Skip to contents

MMRR

MMRR_vignette.Rmd

Multiple matrix regression with randomization (MMRR) 

# Install required packages
mmrr_packages()

If using MMRR, please cite the following: Wang I.J. (2013) Examining the full effects of landscape heterogeneity on spatial genetic variation: a multiple matrix regression approach for quantifying geographic and ecological isolation. Evolution 67(1):3403-3411. DOI:10.1111/evo.12134

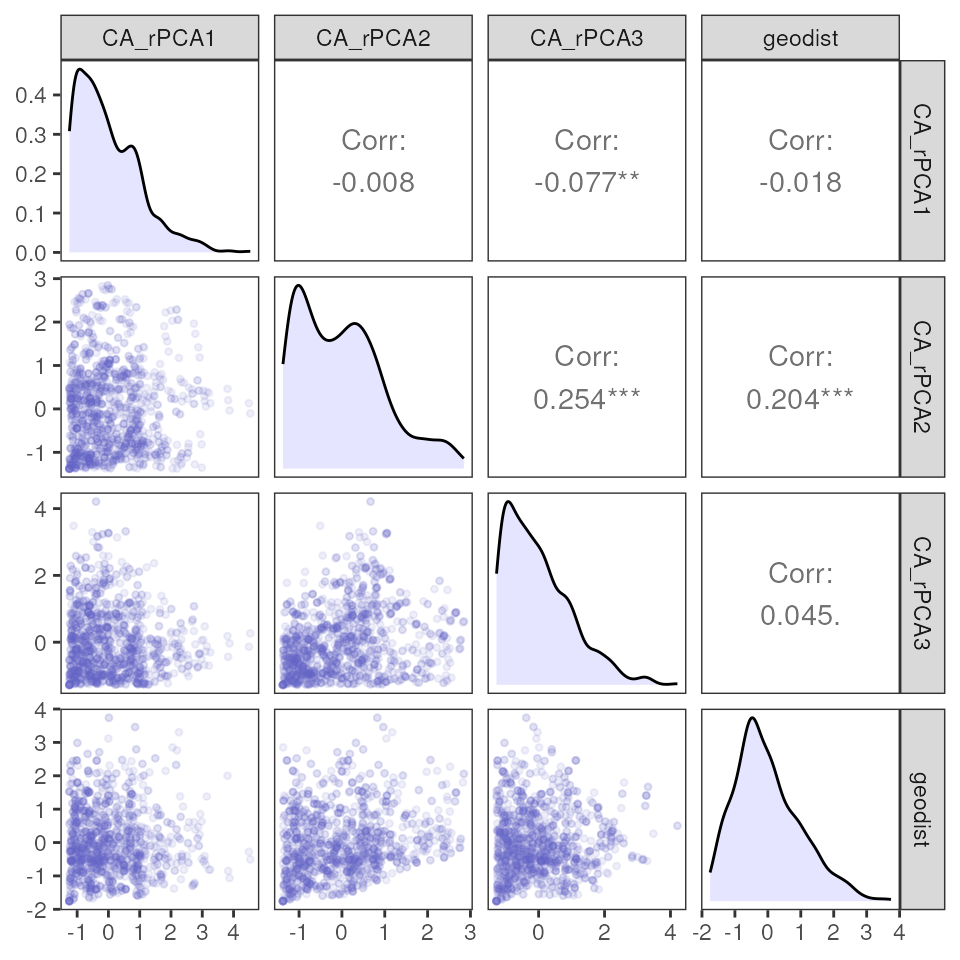
Multiple matrix regression with randomization (Wang 2013) examines how heterogeneity in the landscape (both geographic and environmental) affects spatial genetic variation, allowing a user to determine the relative contributions of isolation by distance (i.e., an association between genetic and geographic distances) and isolation by environment (i.e., an association between genetic and environmental distances). MMRR can provide information concerning how dependent variables (in our case, genetic data) change with respect to multiple independent variables (environmental and geographic distances).

The randomization aspect of MMRR is that significance testing is performed through random permutations of the rows and columns of the dependent matrix (the genetic distances), which is necessary because of the non-independence of values in pairwise distance matrices. Once significance testing is completed, MMRR provides individual regression coefficients and p-values for each dependent variable and a “coefficient ratio,” which is the ratio between regression coefficients, which thus provides an idea of the relative contributions of IBD and IBE in explaining variation in the genetic distances in your data.

There are a few assumptions built into this function that users should be aware of: (1) the coordinates and genetic distance files MUST have the same ordering of individuals; there isn’t a check for this, and (2) this function assumes that each individual has its own sampling coordinates (even if population-based sampling was performed).

Read in and process genetic data

Let’s load the example dataset and extract environmental variables based on our sampling coordinates. To perform MMRR, we need a genetic distance matrix; please refer to the genetic distances vignette for information on how to generate this in algatr using a vcf file.

load_algatr_example()
#> 
#> ---------------- example dataset ----------------
#>  
#> Objects loaded: 
#> *liz_vcf* vcfR object (1000 loci x 53 samples) 
#> *liz_gendist* genetic distance matrix (Plink Distance) 
#> *liz_coords* dataframe with x and y coordinates 
#> *CA_env* RasterStack with example environmental layers 
#> 
#> -------------------------------------------------
#> 
#> 
Y <- as.matrix(liz_gendist)

Process environmental data

Let’s calculate environmental distances with our extracted environmental values using the env_dist() function, and add on geographic distances to this matrix using the geo_dist() function. For more information on how these two functions work, please refer to algatr’s environmental data processing vignette.

# Extract values from our environmental raster (CA_env)
env <- raster::extract(CA_env, liz_coords)
# Calculate environmental distances
X <- env_dist(env)
# Add geographic distance to X
X[["geodist"]] <- geo_dist(liz_coords)

Run MMRR

We can run MMRR using the mmrr_run() function. We can either run the full model (with no variable selection) by setting model = "full", or by running a variable selection procedure using backwards elimination by setting model = "best" within this function. The arguments to mmrr_run() are as follows:

  • Y: matrix of genetic distances

  • X: matrix of environmental distances (including geographic distances) at each sampling coordinate

  • nperm: number of permutations to perform

  • stdz: whether matrices are standardized

MMRR with all variables

First, let’s run the full MMRR model with all variables included (i.e., no variable selection).

set.seed(10)
results_full <- mmrr_run(Y, X, nperm = 99, stdz = TRUE, model = "full")

The results from running the “full” MMRR model contains four elements:

  • coeff_df: a dataframe with statistics relating to each variable’s distance related to genetic distance, including coefficient values for each environmental variable and geographic distance

  • mod: a dataframe containing statistics for the results of the model, including an R^2 value, and F statistics

  • X and Y: the input data

MMRR with model selection

Now, let’s run MMRR with variable selection.

# Run MMRR with all variables
set.seed(01)
results_best <- mmrr_run(Y, X, nperm = 99, stdz = TRUE, model = "best")

Once again, the results from running mmrr_run() with model selection contains the same elements as “full”, except that the “best” model result now also has an X_best element, which contains values for significant variables; in this case, the only significant variable found was geographic distance. You can also see that the coeff_df element is reduced from all four variables to only those variables that were significantly associated with genetic distance (in the test example case, only geographic distance).

Visualizing MMRR results

Plotting MMRR results with mmrr_plot()

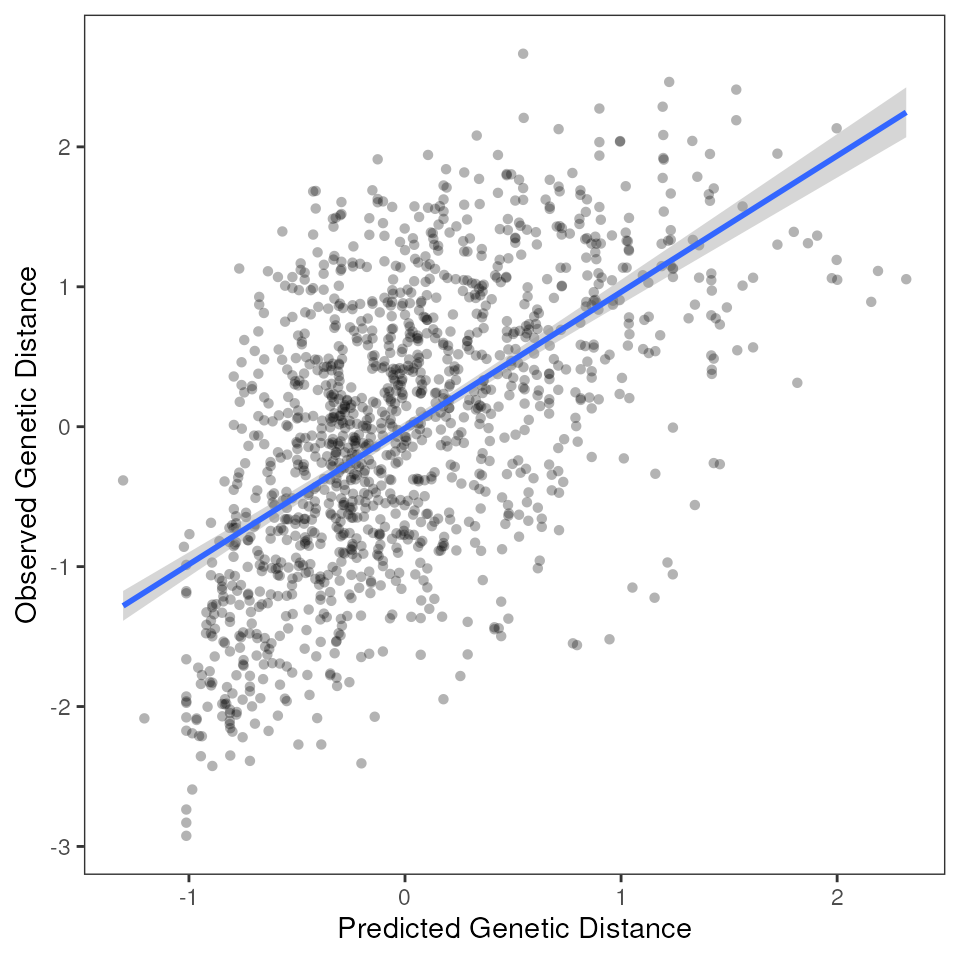
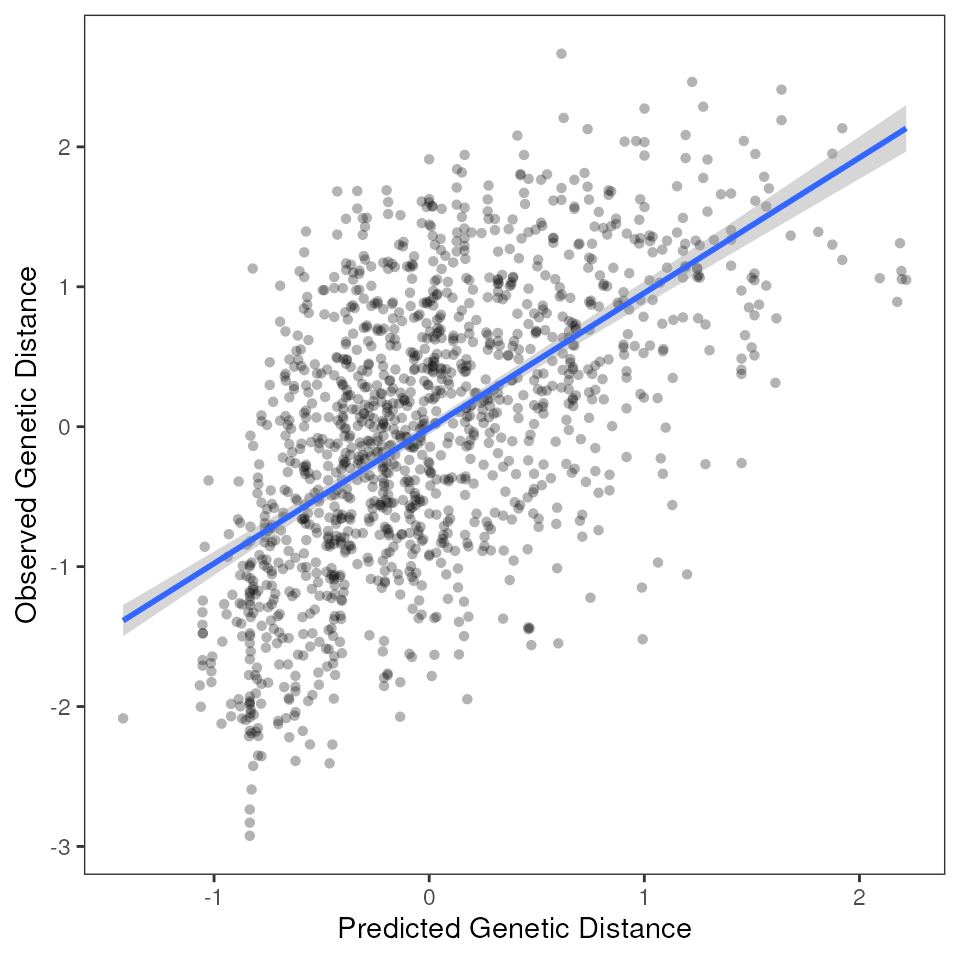
Let’s take a look at the results from our MMRR analyses above. We can produce several plots to visualize results with the mmrr_plot() function, including plotting single variable relationships (plot_type = "vars"), plotting the fitted relationship that compares predicted against the observed genetic distances (plot_type = "fitted"), or plotting covariances between the predictor variables (plot_type = "cov"). Lastly, you can set plot_type = "all" to produce all three of these plots for your MMRR run.

# Single variable plot
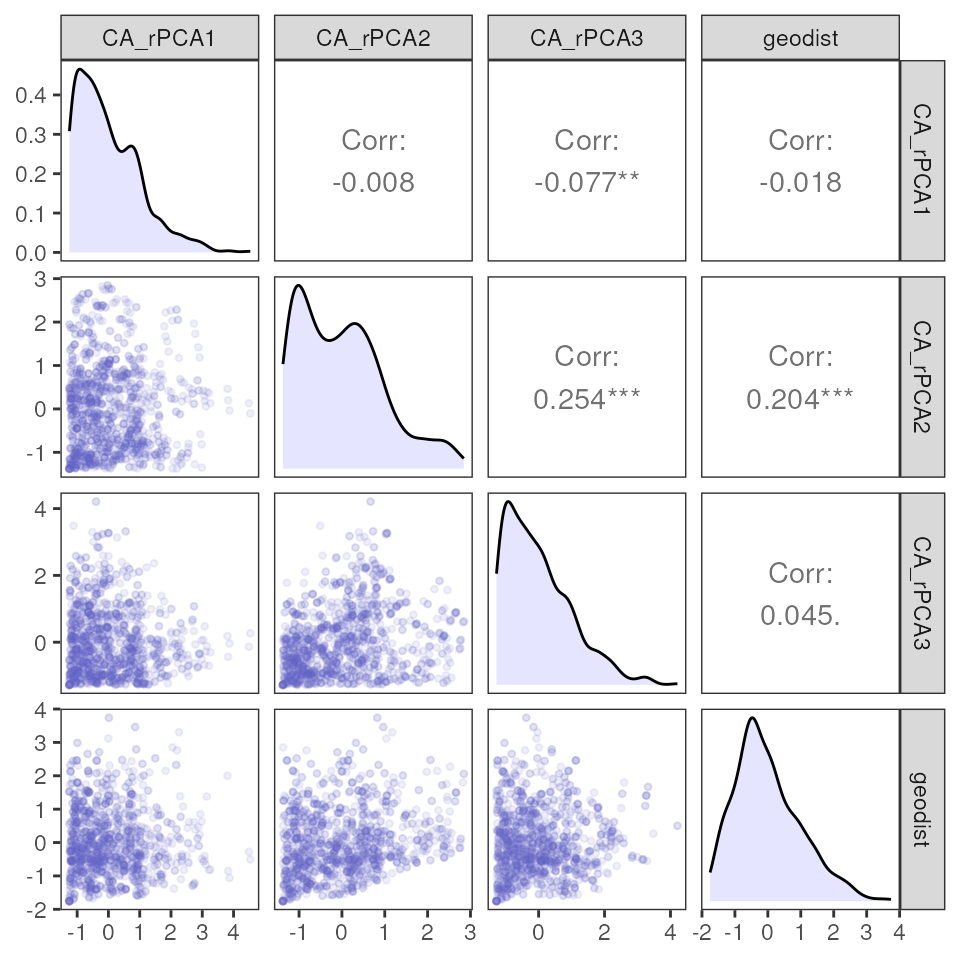
mmrr_plot(Y, X, mod = results_full$mod, plot_type = "vars", stdz = TRUE)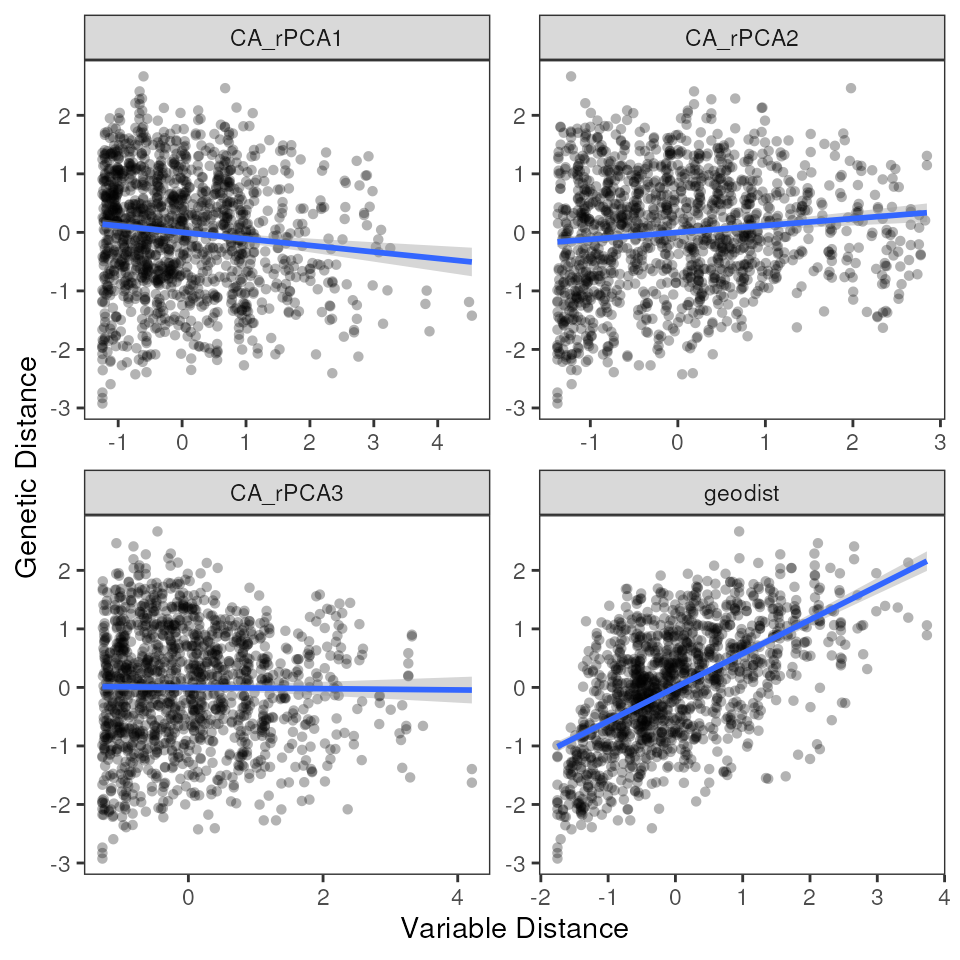

# Fitted variable plot
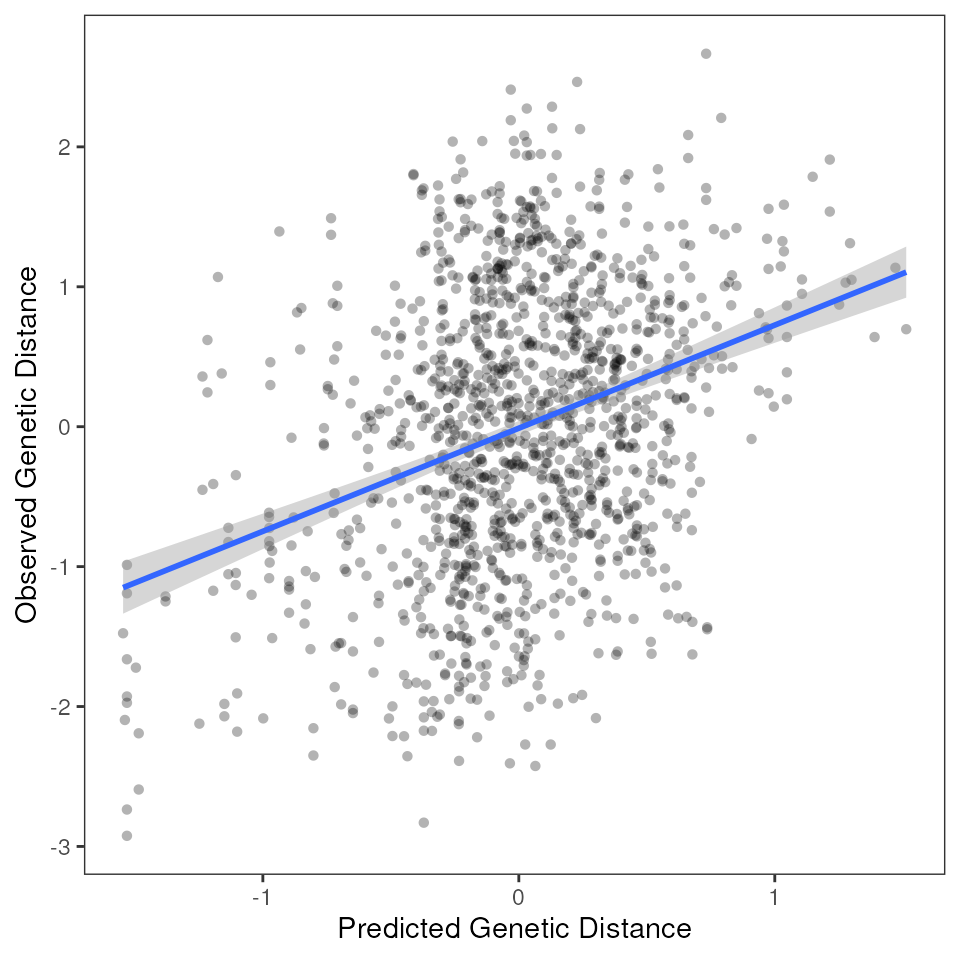
mmrr_plot(Y, X, mod = results_full$mod, plot_type = "fitted", stdz = TRUE)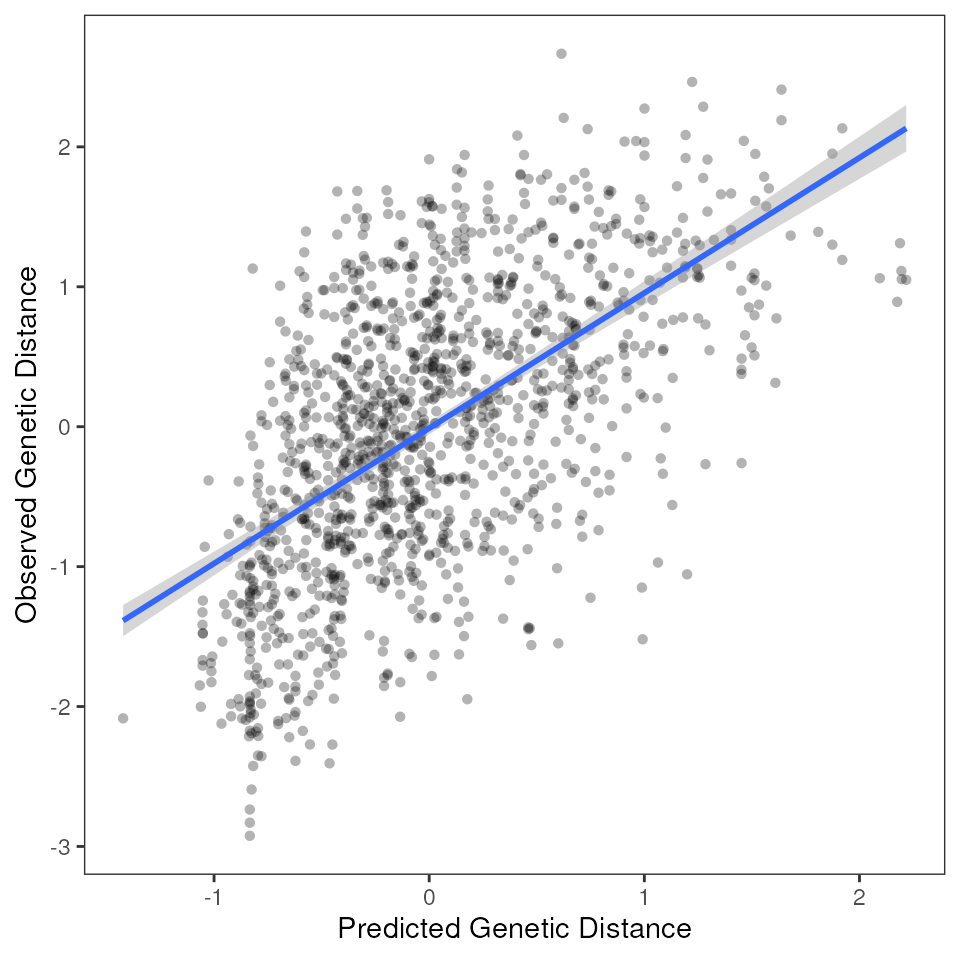

# Covariance plot
mmrr_plot(Y, X, mod = results_full$mod, plot_type = "cov", stdz = TRUE)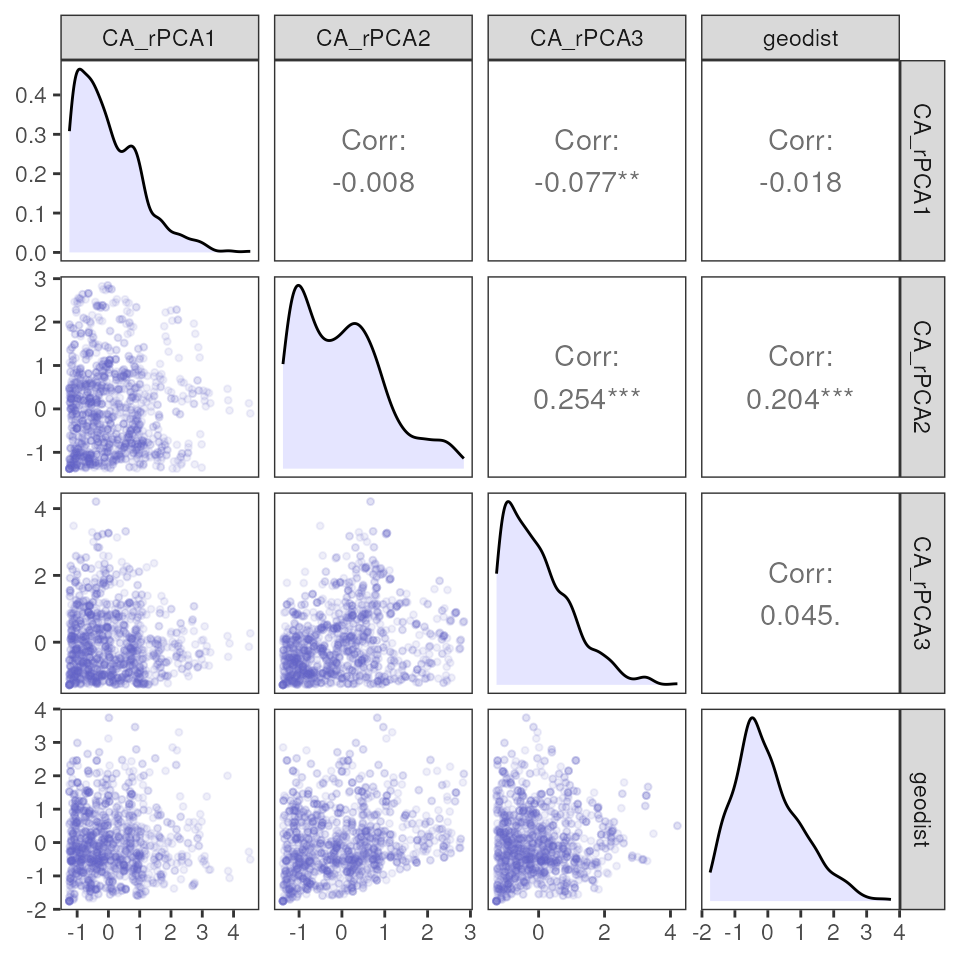
#> Registered S3 method overwritten by 'GGally':
#>   method from   
#>   +.gg   ggplot2

How do the above results compare to those from the “best” model?

mmrr_plot(Y, X, mod = results_best$mod, plot_type = "all", stdz = TRUE)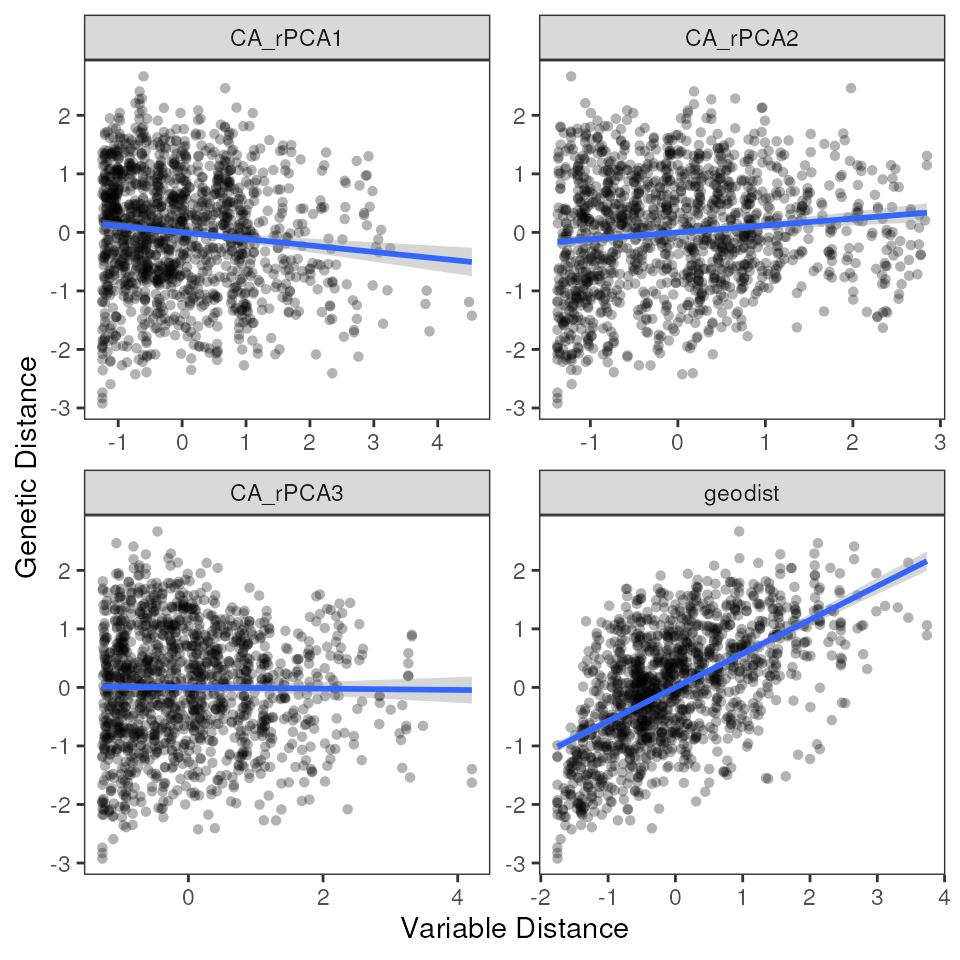

Look at MMRR output statistics with mmrr_table()

We can also take a closer look at the output statistics from our MMRR runs using the mmrr_table() function. This function will also provide summary statistics if we set summary_stats to TRUE (the default). The estimate column contains the coefficients for each of the variables. N.B.: significance values may change slightly due to the permutation procedure.

mmrr_table(results_full, digits = 2, summary_stats = TRUE)
var estimate p 95% Lower 95% Upper
CA_rPCA1 −0.10 0.06 −0.14 −0.07
CA_rPCA2 0.01 0.77 −0.03 0.05
CA_rPCA3 −0.05 0.36 −0.08 −0.01
geodist 0.58 0.01 0.54 0.61
Intercept 0.00 0.01 −0.04 0.04
R-Squared: 0.35


F-Statistic: 181.28


F p-value: 0.01


Running MMRR with mmrr_do_everything()

The algatr package also has an option to run all of the above functionality in a single function, mmrr_do_everything(). This function runs MMRR while specifying whether a user would like to run variable selection or not (using the model argument), producing a table and all plots automatically. It will automatically extract environmental variables based on coordinates and calculate environmental distances from these data. Users can also choose to include geographic distances within the independent variable matrix by setting geo = TRUE (the default setting). Please be aware that the do_everything() functions are meant to be exploratory. We do not recommend their use for final analyses unless certain they are properly parameterized.

MMRR with all variables 

set.seed(01)
mmrr_full_everything <- mmrr_do_everything(liz_gendist, liz_coords, env = CA_env, geo = TRUE, model = "full")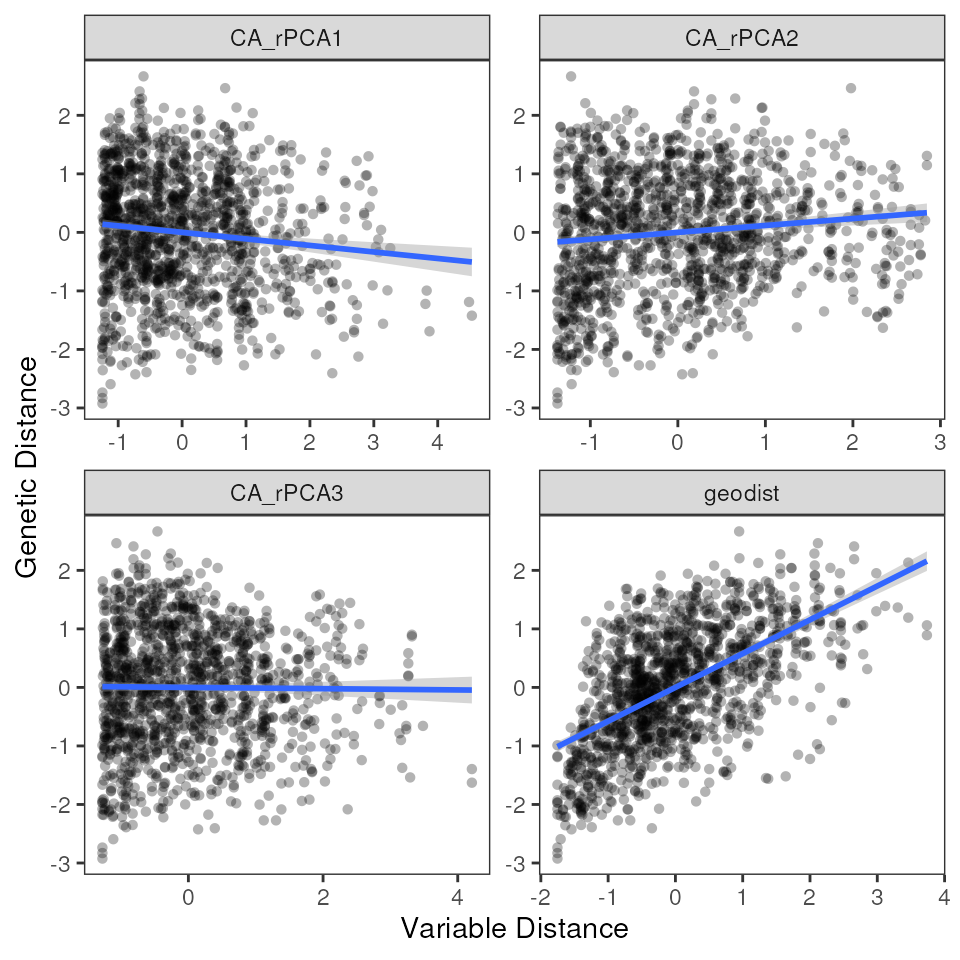
var estimate p 95% Lower 95% Upper
CA_rPCA1 −0.10 0.05 −0.14 −0.07
CA_rPCA2 0.01 0.78 −0.03 0.05
CA_rPCA3 −0.05 0.36 −0.08 −0.01
geodist 0.58 0.00 0.54 0.61
Intercept 0.00 0.00 −0.04 0.04
R-Squared: 0.35


F-Statistic: 181.28


F p-value: 0.00


Extending MMRR’s functionality with resistance distances

The relationships between geographic distance and/or environmental variables on spatial genetic variation result in patterns of isolation by distance (IBD) or isolation by environment (IBE), respectively. However, one other key phenomenon that can occur - and one in which landscape genomicists are often interested in examining - is one in which landscape features act to restrict gene flow, resulting in a pattern known as isolation by resistance (IBR). IBR is typically investigated by first generating a resistance surface which provides information about how the landscape “resists” gene flow given the study organism. Then, given the resistance surface, resistance distances can be calculated using (once again) a variety of methods, but most typically use circuit theory to model connectivity across the landscape.

The resistance surface can be generated using species distribution models, habitat suitability models, or other types of approaches that simulate forward evolution given sampling localities and genotypes (e.g., resistanceGA; Peterman 2018). Building a reliable resistance surface can be quite complex, requiring many decisions on the part of the researcher and, in some cases, extensive parameterization and model testing to generate this type of surface. These sets of decisions are precisely why algatr does not explicitly implement any IBR methods, but below we describe one way in which the package can be extended to do so.

As was briefly mentioned in the environmental data vignette, the geo_dist() function is able to calculate resistance-based distances, largely using the gdistance package (van Etten 2017). Importantly, a user must provide a resistance surface using whichever their preferred method is by specifying the lyr argument. The function then creates a transition surface and calculates circuit distances (random-walk commute distances) using the gdistance::commuteDistance() function.

Although algatr does not have the explicit functionality to quantify and visualize IBR, we can investigate IBR using MMRR given that this method conducts a multiple Mantel test given some distance metric. Thus, it is possible to run geo_dist() specifying lyr with your resistance raster and use the resulting distances as input into MMRR. The following is a toy example of how this could be done. For this example we’ll pretend our resistance surface is one of our environmental layers (where greater values indicate more resistance) and use it to calculate our resistance distances.

# here we aggregate the layer for computational speed
lyr <- aggregate(CA_env$CA_rPCA1, 50)
plot(lyr)
points(liz_coords)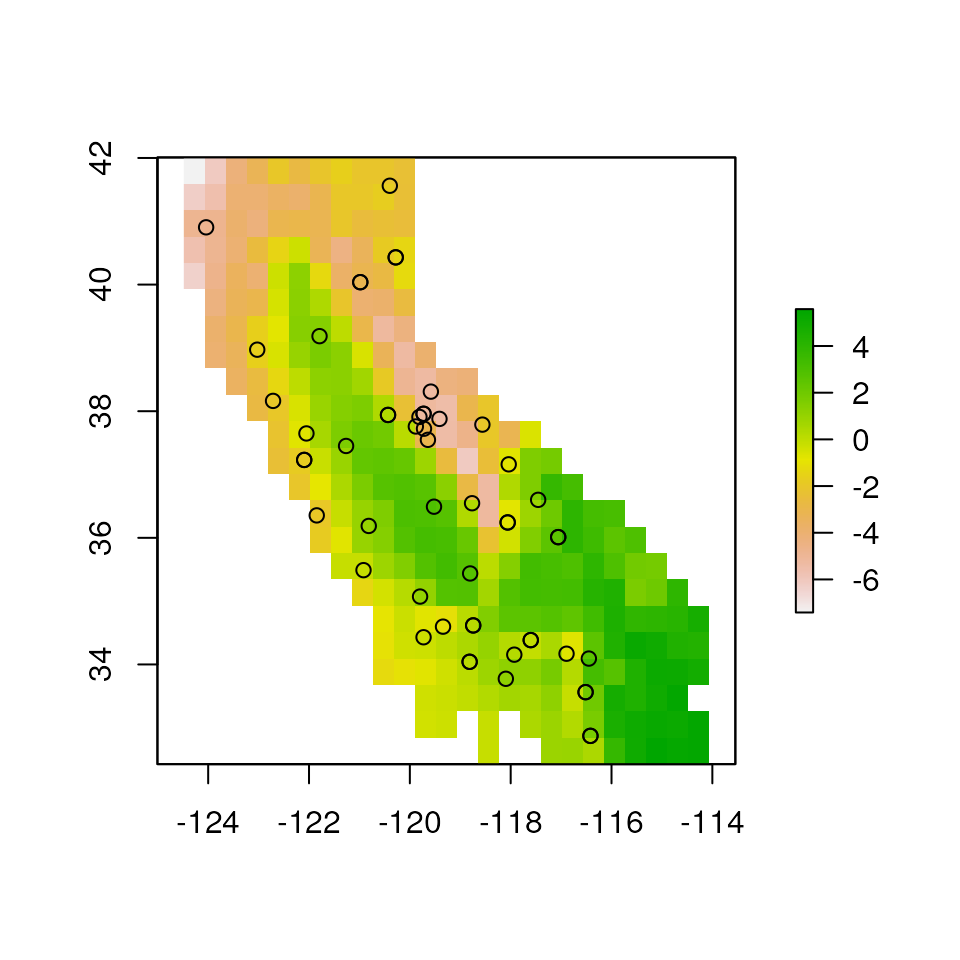


# Recreate MMRR input with resistance distances
# Calculate environmental distances
X <- env_dist(env)
# Add geographic distance to X
X[["resistdist"]] <- geo_dist(liz_coords, type = "resistance", lyr = lyr)
#> Calculating resistance distances... This can be time consuming with many points and large rasters.

Now, we can run MMRR as we did above but including resistance-based distances in our input data.

# Run MMRR with resistance distances
results_resist <- mmrr_run(Y, X, nperm = 99, stdz = TRUE, model = "full")
mmrr_plot(Y, X, mod = results_resist$mod, plot_type = "all", stdz = TRUE)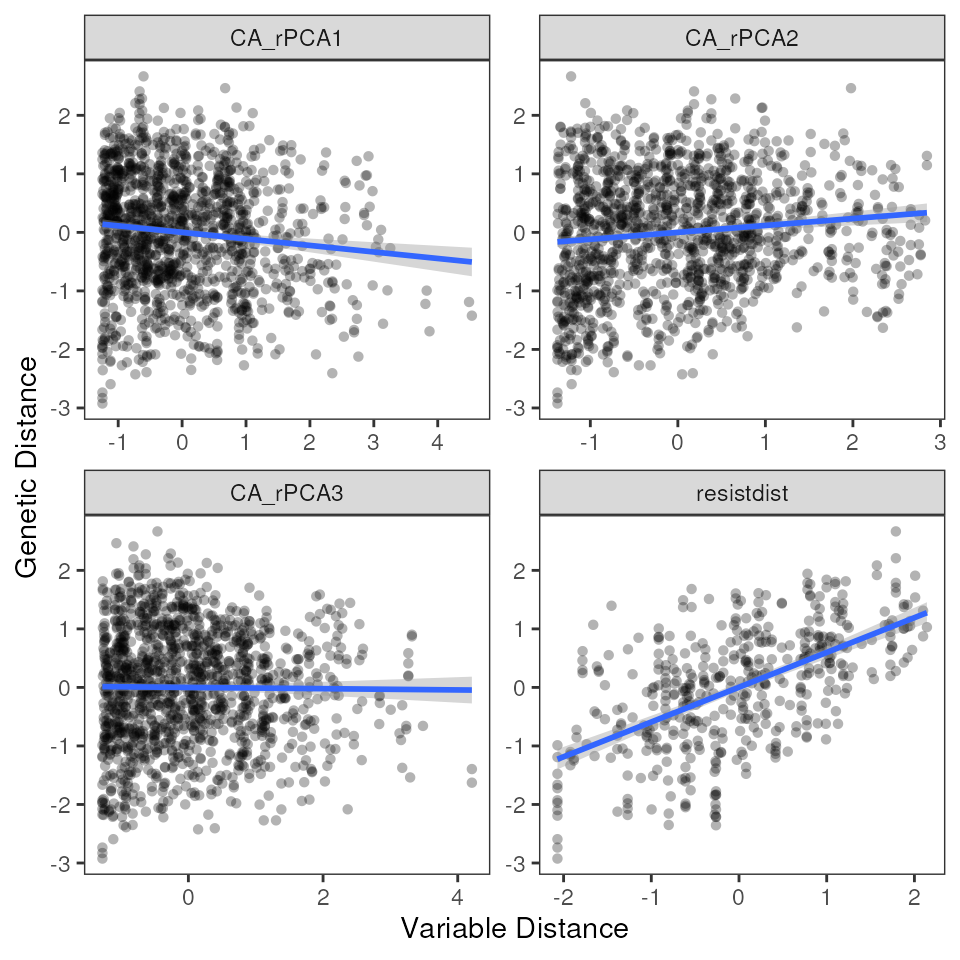

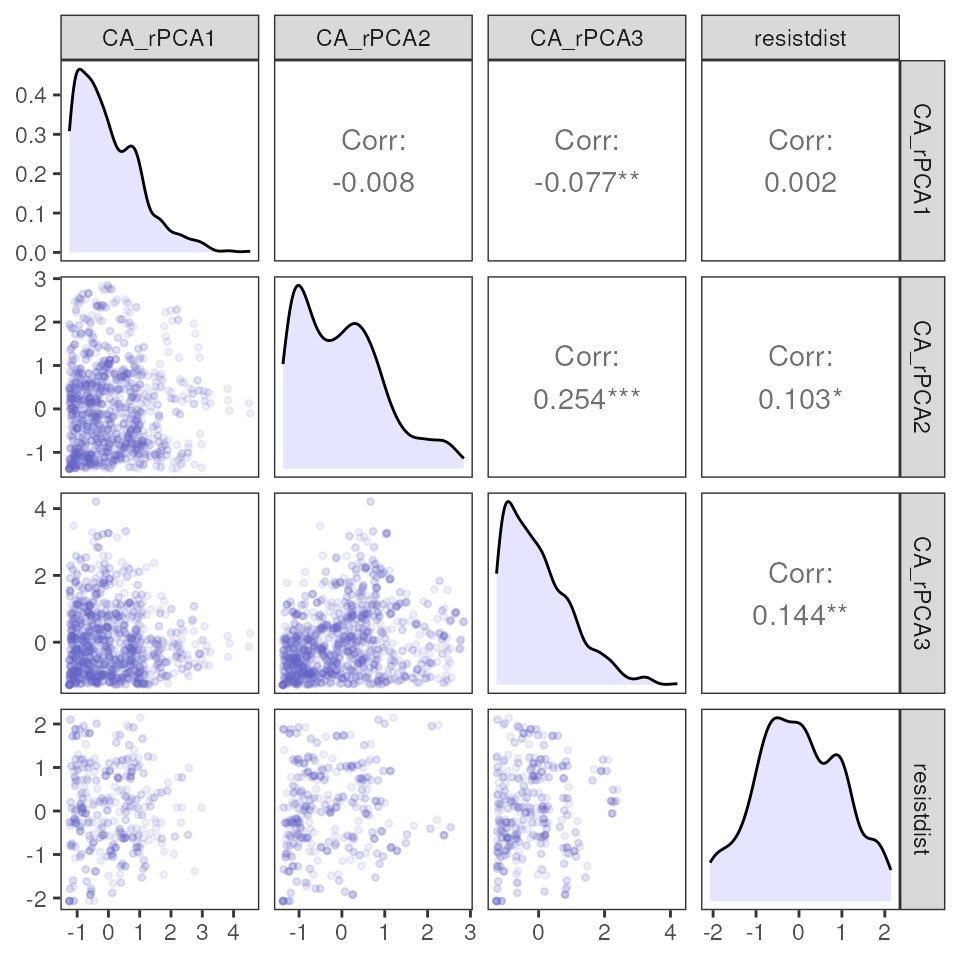
mmrr_table(results_resist)
var estimate p 95% Lower 95% Upper
CA_rPCA1 −0.05 0.39 −0.12 0.02
CA_rPCA2 0.20 0.01 0.12 0.28
CA_rPCA3 0.12 0.15 0.05 0.20
Intercept 0.09 0.24 0.02 0.15
resistdist 0.56 0.01 0.50 0.62
R-Squared: 0.40


F-Statistic: 76.62


F p-value: 0.01


Additional documentation and citations

Citation/URL Details
Manuscript with method Wang 2013 Paper describing MMRR method
Associated code MMRR tutorial Walkthrough of MMRR